CLASE # 3

TERCERA CLASE

Seguimos hablando sobre la matemática computacional,las características principales de la numeracion decimal que son:

• conjunto de números (0,1,2,3,4,5,6,7,8,9)
• Pocisiom
• Multiplicador (10)

El profesor nos enseño como escribir los numeros en sus diferentes bases:

• base 10
• Nibbel
• Octal
• Hexadecimal
• Binarios

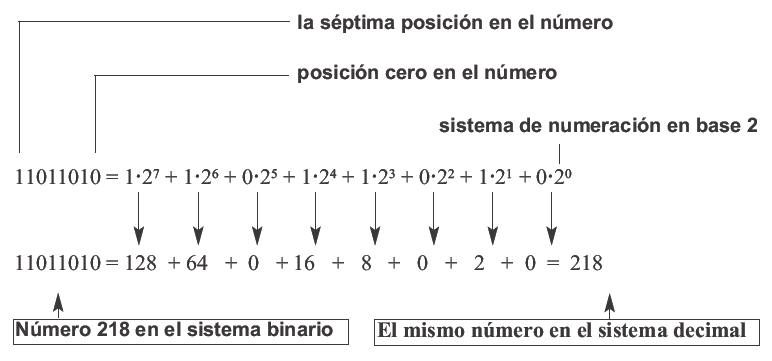
como pasar de una base a la otra y sobre todo para escribir los números en binarios ya que en los computadores se utilizan para entrada y salida de información o datos.

	0hex	=	0dec	=	0oct		0	0	0	0
	1hex	=	1dec	=	1oct		0	0	0	1
	2hex	=	2dec	=	2oct		0	0	1	0
	3hex	=	3dec	=	3oct		0	0	1	1
	4hex	=	4dec	=	4oct		0	1	0	0
	5hex	=	5dec	=	5oct		0	1	0	1
	6hex	=	6dec	=	6oct		0	1	1	0
	7hex	=	7dec	=	7oct		0	1	1	1
	8hex	=	8dec	=	10oct		1	0	0	0
	9hex	=	9dec	=	11oct		1	0	0	1
	Ahex	=	10dec	=	12oct		1	0	1	0
	Bhex	=	11dec	=	13oct		1	0	1	1
	Chex	=	12dec	=	14oct		1	1	0	0
	Dhex	=	13dec	=	15oct		1	1	0	1
	Ehex	=	14dec	=	16oct		1	1	1	0
	Fhex	=	15dec	=	17oct		1	1	1	1

Hicimos diferentes conversiones de numeros de una base a otra ejemplos:

(321121)en base cuatro a decimal

 primero se coge el lsb(pocision menos significativa), y se empieza a descomponer hasta llegar a su pocision mas significativa, con el numero 1 de derecha a izquierda se toma el numero y se multiplica por la base que en este caso es 4 y se eleva a cero, luego el segundo numero de derecha a izquierda que en este caso es un 2 se multiplica igual por la base que en este caso es 4 y se eleva a la 1, luego con los otros numeros hacemos lo mismo en el mismo orden de derecha a izquierda vamos tomandolos uno a uno y los multiplicamos por la base que es cuatro y los vamos elevando de acuerdo al orden a la 2, ala 3 y asi sucesivamente hasta llegar al numero mas significativo que es este caso es 3, luego hacemos las respectivas operaciones de multiplicacion y despues vamos sumando los resultados de las multiplicaciones y asi tenemos nuestro numero en base cuatro o (Nibble) expresado ahora en base (10) o decimal.

(321121)= 1 x 4^0 +  2 x 4^1 + 1 x 4^2 + 1 x 4^3 + 2 x 4^4 + 3 x 4^5=

1+8 + 16 + 64 + 512 + 3072 = 3673

Tambien hicimos otras conversiones  de numeros por ejemplo de binario a hexadecimal, para esto  se debe tomar de a cuatro binarios y hallar su representacion en la tabla de equivalencias hexadecimales.

teniendo en cuenta el 8421 que es el valor de los numeros binarios con respecto a su ubicacion.

Representacion Binaria

Dec      8 4 2 1                HEXADECIMAL             OCTAL           NIBBLE

0          0 0 0 0                          0                                    0                        0                           

1          0 0 0 1                          1                                    1                        1                                           

2          0 0 1 0                          2                                    2                        2                              

3          0 0 1 1                          3                                    3                        3                                          

4          0 1 0 0                          4                                    4                       10                                               

5          0 1 0 1                          5                                    5                       11                                          

6          0 1 1 0                          6                                    6                       12                                         

7          0 1 1 1                          7                                    7                       13                                               

8          1 0 0 0                          8                                    10                     14                                               

9          1 0 0 1                          9                                    11                     15                          

10        1 0 1 0                          A                                   12                      16                               

11        1 0 1 1                          B                                   13                      17                        

12        1 1 0 0                          C                                   14                      18                              

13        1 1 0 1                          D                                   15                      19                        

14        1 1 1 0                          E                                   16                       20                                     

15        1 1 1 1                          F                                   17                       21                                      

                                E         2          B

111000101011=  [1110] [0010] [1011]  = E2B en base 16 o hexadecimal

Lo mismo hacemos con la base octal pero no tomamos de a cuatro binarios sino de a tres

                              7        0        5         3                
111000101011= [111] [000] [101]  [011] = 7053 en base 8 o Octal

En base cuatro es igual solo que cogemos de a dos binarios.
                              3      2     0      2    0       3                                                  
111000101011= [11] [10] [00] [10] [10] [11] = 320203 en base 4 o Nibble